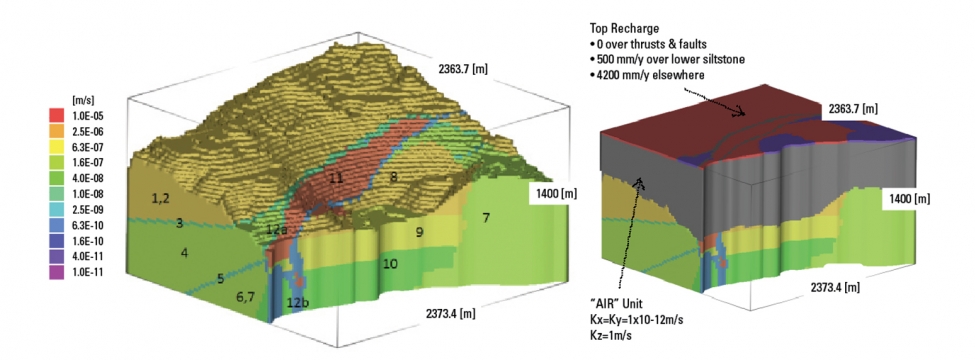
Integrating groundwater pressures into slope stability modelling is an evolving process in mine design. The goal is to carefully match the slope modelling requirements with a somewhat conservative and plausible groundwater scenario while keeping things as simple as possible. The simplest approach is to use 2D cross sections of the pit slope and assess the stability assuming either a hand-drawn or a simulated 2D hydrostatic water table. In some cases, this approach may be sufficient and deemed conservative, but more often it ignores the geological complexities that affect slope performance and cannot correctly represent the potential high pressures found at the toe of pit slopes. The Holy Grail consists of modelling the transient excavation of the full scale pit in 3D, predicting the pore pressures coupled with the geomechanical changes in the rock mass due to unloading (rock mass dilation, etc.). While we never have the data to accuratelyconceptualise and calibrate full pit scale models to this level of complexity, opting for 3D modelling significantly increases the effort and must be therefore chosen cautiously. Specific site conditions may be required such as the influence of a dominant orientation of fractures producing anisotropic flow/ depressurisation, pit geometry, localised sources of recharge, etc.
A major limitation for the 3D modelling used to be the ability of groundwater modelling codes to construct complex geometries such as a pinching geological layer or pit slopes changing over time. The recent advances in commercial software make it possible to provide 3D pore pressure distributions, in both, static or transient conditions, that match the slope geology at limited cost (i.e. time and computer power). The construction of meshes is more flexible and efficient with “unstructured” grids. The geology geometry can be more accurately modelled and again transferred back more accurately to slope modelling to ensure geotechnical and hydrogeological domains match. The alternative block method SRK utilised to allow for geometry matching with complex stability codes such as 3DEC (SRK, 2013) still has some advantages but may quickly become obsolete.
As with much of the modelling we can do today, the codes allow for ever higher complexity to be brought into the analysis. However, the key is still to understand where the groundwater and geomechanical models need to most accurately interact, what portions of the slope are most sensitive to pore pressures (and this will change with time due to natural or induced depressurisation), and what are the data uncertainties and resulting limits of the models. Model sensitivity is an important part of the modelling, and must be used to determine potential uncertainty/probability in whether acceptable depressurisation rates can be achieved to produce stable slopes, or identify the need for more proactive measures (enhanced drain installation programmes, drainage adits, etc.).